Special Issue: Plant Growth and Development

Ann Agric Crop Sci. 2024; 9(6): 1170.

Plant Growth Development and Control in Water-Limited Regions

Zhongsheng Guo^1,2*

¹Northwestern A & F University, Yangling, China

²Institute of Soil and Water Conservation, CAS & MWR, Yangling, China

*Corresponding author: Zhongsheng Guo, Northwestern A & F University, Institute of Soil and Water Conservation, CAS & MWR, 26 Xinong Road, Yangling, Shaanxi Province 712100, China. Tel: ++86-29-87012411; Fax: ++86-29-8701-2210 Email: zhongshengguo@sohu.com

Received: October 21, 2024; Accepted: November 07, 2024 Published: November 14, 2024

Abstract

Man-made vegetation often produces more product and benefit for people’s happy life. But it often has changed the plant resources relationship from dynamic balance relation in origin forest to imbalances, leading to soil degradation, vegetation declines and crop failure or Waste of resources in waterlimited regions. To solve the question, the plant resources relationship must be regulated to get maximum yield and benefits and realize the sustainable use of soil water resource and agriculture high-quality development. Therefore, a novel theory, Resources Use Limit by Plant (RULP) has been developed. For example, RULP is the RULP is the SWRULP, which refers to the amount of water stored in the Maximum Infiltration Depth (MID) at which the soil moisture content in each layer is equivalent to the wilting coefficient. The wilting coefficient is expressed by the wilting coefficient of indicator plants in a plant community. To better understand SWRULP, in the present study, the SWRULP was assessed in a Caragana shrubland and an alfalfa grassland in semiarid loess hilly region. The results showed that the wilting coefficient varied with soil depth, and the SWRULP changed with site conditions and vegetation type. When the soil water resources were equivalent to the SWRULP, the water plant relationship regulation should be considered according to soil water carrying capacity for vegetation in the critical period of plant water relation regulation to make plant grow well and get maximum yield and benefits to realize sustainable use of soil water resource and agriculture high-quality development.

Keywords: Water-limited regions; Plant growth; Severe soil drought; Soil degradation; Wilting coefficient; maximum infiltration depth; Soil Water Resources Use Limit by Plants; Soil water carrying capacity for vegetation

Introduction

After origin forest changed into man-made vegetation, such as plantation, crop, grass or orchard, degraded land become more and more because the plant resources relationship has changed. The sustainable management of degraded land is a critical ecological activity for ensuring the stability of ecosystems [1]. Water movement within the Soil-Plant-Atmosphere Continuum (SPAC) is under the influence of potential gradients. Water flows first from the soil into the roots, then into the leaves, and finally to the atmosphere. Soil water not only influences the physical environments of plant roots but also soil chemical and biological conditions, particularly in waterlimited regions where climate and soil properties are the key factors influencing the plant water relationship. Consequently, plant water relationship plays an important role in plant ecosystem so that soil water management is critical in agricultural systems management.

Since drought is a recurring natural phenomenon, and soil water reservoirs regulate soil water resources, and the effects of drought on plant growth vary with gravity and drought duration in such regions, it is necessary to regulate the relationship since soil drought occurs when the soil water resources reduce to a degree that soil water influences plant growth considerably. Consequently, it is critical to determine the appropriate time based on soil drought degree to begin regulating the plant water relation and the amounts of trees or plants that should be cut when attempting to regulate the plant water relationship [10,18].

Numerous soil water deficit indices have been used to express soil water stress in plants in a given point, such as crop moisture index [30], soil moisture deficit index, evapotranspiration deficit index, and plant water deficit index [35]. But they hardly account for water deficit accumulation or soil water resources in soil body plant root distributed, and they are not appropriate indices for evaluating soil drought severity in forests, grasslands, and farmlands in the waterlimited regions such as the Loess Plateau of China because plant root vertically distributed and suck soil water in the soil body in which the distribution of soil water is often uneven.

Soil Water Resource Use Limit by Plants is a novel theory and a comprehensive soil water deficit index for the determination of whether plants utilize soil water resources sustainably and agriculture high-quality development [12,15-18]. For the better understanding of SWRULP, and to facilitate the sustainable use of soil water resources in water-limited regions, in the present work, SWRULP theory was developed. The objectives of the present study were: (1) to assess changes in wilting coefficient with increasing soil depth; (2) to assess changes in cumulative infiltration depths with increasing time, and (3) to assess the changes of SWRULP with site conditions and vegetation types.

Research Methods

Site Description

The present study was conducted at the Shanghuang Ecoexperiment Station in a semiarid Loess hilly region (35°59'- 36°02' N, 106°26'- 106°30' E) in Guyuan, China, Institute of Soil and Water Conservation of Chinese Academy of Sciences. The altitudes of the Eco-experiment stations range from 1,534 m to 1,824 m. Annual mean rainfall measured between 1983 and 2001 was 415.6 mm with a maximum of 634.7 mm in 1984 and a minimum of 284.3 mm in 1991. Precipitation in the region is absent from Jan. to March and from Nov. to Dec., and the total rainfall in five months was 28.2 mm on average, which accounted for 6.7% of the mean annual precipitation. Th e rainfall in April is 23.1 mm and accounts for 5.6% of the mean annual precipitation, the rainfall in October is 29.8 mm and accounts for 7.2% of the MAP, and the rainfall from June to September is 299.8 mm, which accounts for more than 70% of the mean annual precipitation. The frost-free season spans 152 days. The Huangmian soil, having developed directly from the loess parent materials, consists mainly of loamy porous loess [13] with widespread distribution in the semiarid hilly region of the Loess Plateau. The experimental field selected was located in the 16-year-old Caragana brushland planted in a fish-scale pit in Heici Mountain, and a newly planted Caragana brushland and a wasteland in the middle of Heici Mountain with a slope gradient ranging from 0 to 10°. Saskatoon berries (Amelanchier alnifolia Nutt.) were planted in bench terraces in 2008 while alfalfa (Medicago sativa L.) is sowed on farmland in 2011. The major plant species under the bushes included Stipa bungeana Trin., Heterpoappus attaicus (Eilld). Novpkr., Artemisia giraldi Pamp., and Thymus mongolicus Ronn.

Observation and Measurement Methods

Rainfall at the study site was measured using standard rain gauges, which were approximately 50 m from the Shanghuang Eco-experiment weather station, which is part of the Guyuan Ecoexperiment weather station under the Institute of Soil and Water conservation of the Chinese Academy of Sciences. Soil moisture content, plant root distribution, and other plant growth parameters were also determined.

The experimental plots lay on a gentle slope facing east by south with a gradient of approximately 8°. Three sampling pits were dug at the top and middle sections of Heici Mountain, and alfalfa grass samples were collected at the experimental sites for use in investigating soil profiles. The sampling pit dimensions were 1 m2 × 4 m depth, and they were dug on the Caragana shrubland in September 2012 and in the alfalfa grassland in 2015. The undisturbed soil samples were collected in triplicate at depths of 0 -5cm, 20-25 cm, 40-45cm, 80- 85cm, 120- 125cm, 160-165cm, 200-205cm, 240 -245cm, 320-325cm and 380-385 cm with cutting rings (5 cm high, 5 cm inner diameter, and 100 cm3 volume), and the excess soil at the openings on both sides of the ring were cut using a sharp knife, sealed, and then transported to the laboratory for use in subsequent analyses. In addition, 100 g of disturbed soil was collected at each depth for the determination of soil structure at the State Key Laboratory of Soil Erosion and Dryland Farming on the Loess Plateau, China.

The cutting ring method was used to measure soil bulk density, total porosity, capillary porosity, and saturation moisture content. The core samples (undisturbed soil sample) collected were used with cutting rings to measure the soil bulk density, capillary porosity, and non-capillary porosity. The bulk density was determined by ovendrying the cores at 105–110, and the total porosity was calculated as 1-bulk density/soil particles density, assuming that the density of soil particles was 2.65 g/cm3. Non-capillary porosity was the difference between total porosity and capillary porosity. Organic content was measured using the Potassium dichromate volumetric method. The methods for particle size determination generally include direct measurement, dry and wet sieving, settling tube analysis, pipette and laser granulometer, X-ray Sedigraph, and Coulter Counter analyses [26]; however, a Laser granulometer is commonly used for the analysis of the grain sizes of marine sediments. Soil particle sizes were measured using a master sizer 2000 laser particle analyser (Malvern Instruments Ltd., Malvern, UK) and grain size was graded based on the United States Department of Agriculture classification system for particle sizes [24]. Soil water concentrations at different soil suctions (0.1, 0.2, 0.4, 0.6, 0.8, 1.0, 2.0, 4.0, 6.0, 8.0 bar, 1 bar = 0.1×105MPa) were measured using a Hitachi centrifuge (Hitachi Instruments Inc., Tokyo, Japan).Because the Huangmian soil contracted when subjected to centrifuging, the authors measured the degree of shrinking of the samples in the cutting ring using Vernier callipers at different soil suction levels and then calculated the volumetric soil water content. Subsequently, the Gardner empirical formula 0=a S – b was used to fit the data to plot a soil water characteristic curve based on the least square method. The wilting coefficient can be estimated using the equation when the suction is equal to 15 MPa [10].

Rain gauges were installed at the experiment site. On the Caragana brushland, five 100-m2 (5 m in width × 20 m in length) plots were prepared down the slope. Two holes with 5.3-cm diameter were dug using a holesaw in the middle of each experimental plot, and two 4-m long aluminum access pipes were placed in the holes at intervals of 2 m in 2002. The interspaces between the access pipes and the soil were filled with some fine earth to prevent the flow of water through the interspaces. In 2011, the aluminum access pipes were replaced with 8-m long PVC access pipes because the 4-meter-long aluminum tube can only be used to measure the soil moisture content of 0-390 cm soil, while the caragana duck can draw water from the soil depth of more than 400 cm. Three pairs of 8-m long PVC pipes were placed in the holes in the alfalfa grassland. A neutron probe, CNC503A (DR) (Beijing Nuclear Instrument Co., China) was used for the long-term monitoring of the field soil water content because of its high precision in situ [7,40]. Before measuring the volumetric soil water content, the neutron probe was calibrated for the soil in the study area using standard methods [20]. The calibration equation for the soil at the site is y = 55.76 x + 1.89, where y is volumetric soil water content in %, and x is the ratio of the neutron count in the soil to the standard count assuming the calibration equation is the same because the distance and the different of the height among the study sites is small. The measuring depth ranged from 0 to 400 cm over previous five years from 2002 to 2006 and 0 to 800 cm during from 2011 to 2014. Measurements were carried with 15-day time intervals and 20-cm depth intervals to a depth of 360 cm or 760 cm from a depth of 5 cm. The soil water content determined at each depth was considered representative for the soil layer that included the measuring point ± 10 cm depth, excluding the measurement obtained at 5-cm depth, which was considered to represent the 0 to 10-cm soil [42]. The measurements were carried out from mid-April to October or November for five years from 2002 to 2006, and from January to December for three years from 2011 to 2015, which represented to nine years in total.

The measurements were also performed before and after each rain event in the shrubland, since rainfall is a discrete process, and a rain event refers to the time interval between the occurrence of rain during a period that is equal to or greater in duration than a specific threshold: the Minimum Inter-event Time (MIT) [21] and the minimum interevent time was 30 minutes.

Height and diameter of the shrubs growing on the plots were measured and their mean heights and diameters were estimated. A sample shrub with approximately the mean height and diameter of the shrubs on the plots was selected near a side boundary outside each plot. A hole (another soil profile, 1 m long × 1 m wide and 5 m deep) was dug around the base of the shrub. The parts of the shrub 2 cm above the ground were removed, so that the average root diameter was determined by vernier caliper and root density were determined at soil depths of 0 to 10 cm, 10 to 50 cm, 50 to 100 cm, 100 to 200 cm, 200 to 300 cm, 300 to 400 cm, and 400 to 500 cm,

On each plot in the 16-year-old Caragana shrubland planted in a fish scale pit in 1986, 10 sample shrubs were selected to determine plant growth characteristics: height and crown area. Forty sample shrubs were selected in the newly sowed Caragana shrubland and the alfalfa grassland. Because the shape of the Caragana canopy projection area was somewhat elliptical, the maximum horizontal diameter of the crown was measured in two directions perpendicular to each other [42]. Four stems in each sample shrub and 40 stems in each plot were selected. On each plot in the young Caragana shrubland planted by sowing in 2002, 20 stems were selected in each plot. The plant used for the sampling activities were marked with red lacquer at points at which the basic diameters were measured and the heights and stem diameters of the selected shrubs determined and used to estimate the mean heights and mean basic diameters of the selected shrubs. Height, basic diameter, and canopy measurements were performed at 15-day intervals in the course of the growing period from mid-April to October or November for 5 years from 2002 to 2006 and for 4 years from 2011 to 2016, covering a 10-year period in total.

The mathematical model used for calculating SWRULP was as follows:

Here, SWRULP is Soil Water Resources Use Limit by Plants, expressed in mm. MID is maximum infiltration depth in cm. is wilting coefficient at soil depth i in % and D is soil depth in mm.

Statistical Analysis

The influence of planting density on all the parameters measured was assessed using Analysis of Variance performed in SPSS 13.0 (SPSS Inc., Chicago, IL, US), in addition to the effect of pipe position, planting density, and soil depth on soil water content. A regression analysis was then performed to evaluate the relationship between soil water content and moisture suction and root density and soil depth using the least square method. Data were transformed when necessary to obtain linear relationships.

Results

The Changes in Wilting Coefficient with Increasing Soil Depth

Basic soil physical and chemical indicators changed with an increase in soil depth. In the Caragana shrubland in the middle of Heici Mountain, the bulk density of the soil increased slightly from 1.214 g/cm3 in the 20-cm soil layer to 1.266 g/kg in the 320 cm soil layer (Table 1), except for the 5-cm surface soil layer at which the bulk density was 1.191 g/cm3. The bulk density (Wh) based on soil depth, h, can be expressed using the following equation: Wh =0.002h + 1.214, and the determination coefficient, R2, is 0.789. The results suggested that the water holding capacity of the soil was low. depth from 55.06% in the 5-cm soil layer to 52.34% in the 400-cm soil layer. The relationship between total porosity, TP, and soil depth, h, can be expressed as follows: TP= -0.6528 × Ln (h) + 56.164, and the determination coefficient, R2, is 0.9817. The results indicated that correlation between total porosity and soil depth was high and total porosity decreased with an increase in soil depth, which influenced the aeration and water conductivity of soil. In addition, the soil physical clay contents changed with soil depth.

Table 1: Changes of main soil physical and chemical indicators of huangmian soil with soil depth.




  
    Soil depth

      (cm)
    Bulk

      density

      (g·cm-3)
    Organic matter

      content 

      (g·kg-1)
    Clay Particle

      content (%)
    Silt Particle content (%)
    Sand Particle content

      (%)
     
      Physical

        clay

        content

        (%)
    Total Porosity (%)
    Capillary Porosity (%) 
    Non-

      capillary Porosity

      (%)
  
  
    5
    1.19
    6.86
    13.76
    65.68
    20.56
    24.92
    55.06
    35.01
    20.05
  
  
    20
    1.21
    3.69
    13.19
    68.67
    18.14
    23.17
    54.19
    33.89
    20.30
  
  
    40
    1.22
    3.10
    10.99
    71.63
    17.38
    21.55
    53.77
    34.21
    19.56
  
  
    80
    1.23
    3.00
    11.94
    70.39
    17.67
    20.99
    53.43
    34.07
    19.36
  
  
    120
    1.25
    2.62
    11.42
    68.00
    20.58
    21.58
    52.98
    33.43
    19.55
  
  
    160
    1.24
    2.56
    10.75
    67.73
    21.52
    20.05
    53.06
    33.92
    19.14
  
  
    200
    1.25
    2.52
    11.60
    71.20
    17.20
    20.28
    52.75
    33.89
    18.86
  
  
    280
    1.26
    2.61
    11.28
    72.34
    16.38
    22.29
    52.30
    34.24
    18.06
  
  
    320
    1.27
    2.50
    12.47
    70.93
    16.60
    22.73
    52.23
    34.22
    18.01
  
  
    400
    1.26
    2.58
    12.57
    71.51
    15.92
    22.50
    52.34
    35.04
    17.30



Table 1: Changes of main soil physical and chemical indicators of huangmian soil with soil depth.

Considering the Caragana shrubland as an example to demonstrate the change in soil water content with an increase in soil depth, see Figure 1. For example, the volumetric soil water content dropped from 30.5 % to 9.1% with an increase in 0-5 cm soil water suction from 0.01×105 MPa to 8.0 ×105 Pa. The relationship between volumetric soil water content, 0 and soil water suction, S, is expressed as follows: 0 = aS-b

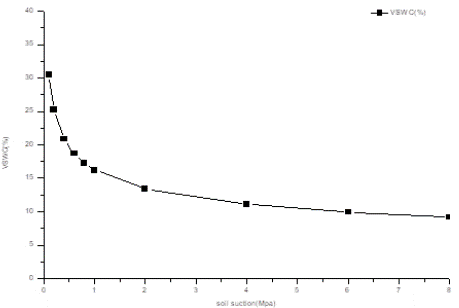
Figure 1: The soil water suction changes with volumetric soil water content (VSWC) in caragana shrubland.

    
    
    Figure 1: The soil water suction changes with volumetric soil water content
(VSWC) in caragana shrubland.

Where 0 is soil water constant and S is soil water suction. Based on the relationship between 0 and S, the wilting point at a water suction of -15×105 Pa can be estimated. The determination coefficient, R2, changes from 0.961 at 200 cm to 0.987 at 310 -330 cm soil depth. The major changes in soil water constants with an increase in soil depth are listed in table 1. At a water suction of -0.33×105 Pa, field capacity dropped from 28.1% at 0-10 cm soil depth to 17.9 % at 150-170 cm soil depth, and then increased gradually to 21.8% at 380-400 cm soil depth. In addition, the wilting point at a water suction of -15×105Pa decreased from 10.3 % at 5 cm to 7.1% at 160 cm and then rose gradually to 8.4% at 380-400 cm soil depth.

Changes in Cumulative Infiltration Depths with Time

During infiltration into the soil, the water that infiltrates the soil surface was partitioned into two components: the increase in the soil water storage and infiltration depth. Downslope interflow was low because the porosity of Huangmian soil is high, its vertical structure is almost homogeneous, and there was no impermeable soil layer in the soil profile (Table 2). When a slope was gentle and the soil water content was less than saturated water content during infiltration, the difference in outflow and inflow of downslope interflow per unit volume of soil was low and less than the error range. Therefore, the difference was disregarded and the soil water content in the soil layers from the surface to the wetting front was less than the saturated soil content.

Table 2: The changes of field capacities and wilting coefficient with soil depth.




  
    Soil depth    (cm)
    Soil water characteristic curve
    determination coefficient, R2
    Field capacity

      (%)
    wilting    coefficient

      (%)
  
  
    0-5
    0 = 0.115S-0.262
    0.98
    28.11
    10.34
  
  
    20-25
    0 = 0.100S -0.257
    0.98
    24.03
    9.01
  
  
    40-45
    0 = 0.089S -0.252
    0.99
    21.02
    8.04
  
  
    80-85
    0 = 0.081S -0.246
    0.98
    18.75
    7.33
  
  
    120-125
    0 = 0.081S -0.242
    0.98
    18.49
    7.34
  
  
    160-165
    0 = 0.078S -0.243
    0.99
    17.87
    7.07
  
  
    200-205
    0 = 0.082S -0.245
    0.96
    18.91
    7.42
  
  
    240-245
    0 = 0.084S -0.244
    0.98
    19.31
    7.61
  
  
    320-325
    0 = 0.089S -0.247
    0.99
    20.67
    8.05
  
  
    400-405
    0 = 0.093S -0.250
    0.98
    21.82
    8.40



Table 2: The changes of field capacities and wilting coefficient with soil depth.

The soil water supply (mm) for one rain event can be determined using the following formula:

where I(t) was soil water supply in mm SWR. The upper limit of the integral is the soil water infiltration depth for one rain event, l, for a rain event in cm or m and the lower limit of the integral zero. The infiltration depth for a rain event can be obtained using the two curves method [10,15] (Figure 2a) i.e., if we measure the dynamics of soil water contents with soil depth before a rain event considering the forecast of weather report and then measure the dynamics of soil water content with soil depth after the rain event, the infiltration depth for a rain event is equal to the distance from the surface to the crossover point between two soil water distribution curves with depth measured in the soil profile before a rain event and after the rain event (or an infiltration process). For example, there is a rain event from August 16-18, 2013. The precipitation was 52.5 mm and the joint location between two soil water distribution curves was 80 cm, which was in the 70–90-cm range. Therefore, the infiltration depth was 90 cm (Figure 2a).

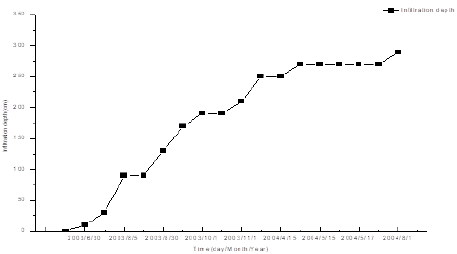
Figure 2: Maximal Infiltration depth in the caragana shrubland. A) Two-curve method for estimating the infiltration depth and soil water supply for one rain event (Top picture); B) The changes of accumulative infiltration depth with time in the caragana shrubland (Below picture).

    
    
    Figure 2: Maximal Infiltration depth in the caragana shrubland. A) Two-curve
method for estimating the infiltration depth and soil water supply for one rain
event (Top picture); B) The changes of accumulative infiltration depth with
time in the caragana shrubland (Below picture).

Over time, the infiltration was divided into two stages: rainfall infiltration generally occurring during a rain event and inter-rain infiltration, the cumulative infiltration (Chowdary et al., 2006), or reinfiltration [6]. If we measure the soil water content dynamics based on soil depth at different time points during a long term infiltration process, we can analyze the change of the cumulative infiltration depth with increase in time, and estimate MID, which is the maximum cumulative infiltration depth, using a series of twocurve methods [15]. The MID is equivalent to the distance from the surface to the deepest crossover point in two contiguous soil water distribution curves with soil depth in the soil profile at the beginning and the end of an extended period or a long-term infiltration process, which is generally more than one rain event. During the experiment from 2002 to 2016, infiltration depth for one rain event increased with an increase in the amount of precipitation and duration, and the cumulative infiltration depth increased with an increase in annual precipitation. Th e precipitation in 2003 was 623.3 mm, which was close to the maximum rainfall record of 634.7 mm in 1984, and the MID during the period from July 5 to August 1, 2004, was 290 cm (Figure 2b). According to the results of a study of SWRULP using a similar method in 2018, the MID in Red plum apricot forest near Caragana shrubland was also 290 cm. The root system is a key organ by which plant absorb water from the soil. In the Caragana shrubland at the middle of Heici Mountain, Caragana roots develop rapidly and exhibit a high capacity to absorb water from considerable depths. The two-curve method can also be used to determine the soil water use depth of Caragana root following the measurements of the dynamics between soil water content and soil depth before and after a period (Figure 3a). One-year-old Caragana shrubs can absorb water from 2.3-m soil layers and the roots of two-year-old Caragana shrubs extended to 260 cm and can absorb water from 330-cm soil layers since the soil depth from which plants absorb water is equivalent to the root distribution depth plus soil depth, which is influenced by roots in which there is not root. This is some soil body range in which there is no root distribution but what root suck water can influence the soil water content by changing the gradient of soil water potential nearby leads to the movement of soil water, thus changing the soil water content. Four- to five-year-old Caragana shrubs can absorb water from soil layers at depths greater than 400 cm, while 16-yearold Caragana roots were observed growing at the bottom of a 500-cm deep hole at the study site with the 16-year-old Caragana shrubs in the present study, suggesting that the roots of Caragana can reach depths greater than 500 cm.

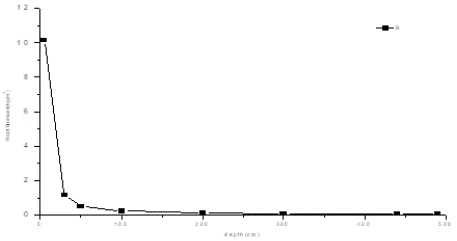
Figure 3: Dynamics of soil water content with time in caragana shrubland. A) the dynamics of soil water content with soil depth in 1–5-year-old caragana shrub; B) the dynamics of root biomass with soil depth in 16-year-old caragana shrub. VSWC is volumetrical soil water content.

    
    
    Figure 3: Dynamics of soil water content with time in caragana shrubland. A)
the dynamics of soil water content with soil depth in 1–5-year-old caragana
shrub; B) the dynamics of root biomass with soil depth in 16-year-old
caragana shrub. VSWC is volumetrical soil water content.

Although 16-year-old Caragana could absorb water from depths as great as 5 m, the roots were mainly distributed in the upper soil layers from the surface to 200 cm, and the density of 1.9 kg/m2 in the 0 to 200-cm soil layers accounted for 88.5% of the total density in the shrubland. The root distribution changed with an increase in soil depth at the 380-400-cm soil layer, as illustrated in Figure 3b. The majority of the root density decreased from 8.6 kg/m2 in the 0–10-cm soil layer to 0.04 kg/m2 in the 350-370 cm soil layer, but most of roots were distributed in the 0 to 200-cm soil layer.

The relationship between root density (RB, kg/m2) and soil depth (H, cm), therefore, can be expressed as follows:

RB=61.464H-1.1808 R2=0.9962 (5)

Wilting coefficient is the water content at -15×106 Mpa, and soil water influences Caragana grow considerably when soil water equals wilting coefficient in given place. When the soil water content in the MID is equal to the wilting point and there is no adequate water supply from precipitation, most Caragana leaves change color and fall earlier than normal during the growing season, which was the case on the August 5, 2003, and Caragana plants almost ceased growing, even when the roots extended to depths greater than 500 cm and could absorb some water from soil layers greater than 290 cm. The above observations suggested that the total amount water that Caragana roots absorbed from soil per unit time did not satisfy the plant transpiration requirements even though Caragana roots could absorb water from the soil layer deeper than 500 cm. The soil water resources in the MID was 222.8 mm, which is the SWRLP in Caragana shrubland.

Height growth trend fitted the logistic formula [42]. As Caragana grew, the soil water resources reduced by 50 mm from 387.3 mm to 337.3 mm in 2002, and then increased by 111.3mm to 448.9 mm because 2003 was a wet year, and then reduced by 119.8 mm to 329.3 mm in 2004, by 0.2 mm to 328.8 mm in 2005, and by 106.1 mm to 222.7 mm in 2006, even though there were some increases after rain events (Figure 4b). Plant height and diameter increased; however, the yearly increments in height and basic diameter decreased from 14.1 cm and 2.7 mm in 2002 to 8.6 cm and 0.6 mm in 2003, to 4.75 cm and 0.6 mm in 2004, to 10.8 cm and 0.19 mm in 2005, and to 4.3 cm and 0.9 mm in 2006, respectively (Figure 4c) potentially because the precipitation in 2006 was 304 .7 mm, which was close to the lowest value of 284.3 mm (Figure 4a).

Changes in Soil Water Resources Use limit by Plants with Vegetation Types and Site Conditions

The wilting coefficient, saturated water content and water storage at different soil layers and their changes with increasing soil depth under different site conditions and vegetation.

These results indicated that SWULP in different site condition and vegetation was different because the soil textures and organic matter contents were different in different sites and under different types of vegetation. The SWRLP in Caragana shrub at the middle of the Heici Mountain was 222.8 mm, see table 3 and the SWRLP at the top of the Heici Mountain it was 252.8 mm, see table 4 and 220.8 mm in alfalfa grassland, see table 5, assuming the MID was 290 cm. The SWRULP is 212.7 mm in Red plum apricot forest in 2018, which indicated that SWRULP changes with site conditions and vegetation type.

Table 3: The SWRLP in caragana shrubland at the middle of the Heici mountain.




  
    Measuring point depth (cm)
    Representing soil layer (cm)
    Wilting coefficient (%)
    Saturated water content (%)
    Water storage in the representing soil    layer (mm)
  
  
    5
    0-10
    10.34
    58.09
    10.34
  
  
    20
    10-30
    9.01
    56.42
    18.02
  
  
    40
    30-60
    8.04
    52.04
    24.12
  
  
    80
    60-100
    7.33
    46.98
    29.32
  
  
    120
    100-140
    7.34
    44.12
    29.36
  
  
    160
    140-180
    7.07
    42.88
    28.28
  
  
    200
    180-220
    7.42
    47.1
    29.68
  
  
    240
    220-280
    7.61
    46.5
    45.66
  
  
    320
    280-290
    8.05
    52.26
    8.05
  
  
    SWRLP
    0-290
     
     
    222.8



Table 3: The SWRLP in caragana shrubland at the middle of the Heici
mountain.

Table 4: The SWRLP in caragana shrubland planted in the fish scale pit at the top of the Heici mountain.




  
    Measuring point depth (cm)
    Representing soil layer (cm)
    Wilting coefficient (%)
    Saturated water content (%)
    Water storage in the representing soil    layer (mm)
  
  
    5
    0-10
    10.32
    50.64
    10.32
  
  
    20
    10-30
    9.79
    53.19
    19.58
  
  
    40
    30-60
    8.88
    54.16
    26.64
  
  
    80
    60-100
    8.13
    52.38
    32.52
  
  
    120
    100-140
    8.08
    54.09
    32.32
  
  
    160
    140-180
    7.67
    52.47
    30.68
  
  
    200
    180-220
    8.74
    54.6
    34.96
  
  
    240
    220-260
    9.54
    56.38
    38.16
  
  
    320
    260-290
    9.22
    54.88
    27.66
  
  
    SWRLP
     
     
     
    252.84



Table 4: The SWRLP in caragana shrubland planted in the fish scale pit at the
top of the Heici mountain.

Table 5: The SWRLP in alfafa grass at the farmland.




  
    Measuring point depth (cm)
    Representing soil layer (cm)
    Wilting coefficient (%)
    Saturated water content (%)
    Water storage in the representing soil    layer (mm)
  
  
    0
    0-10
    7.07
    37.75
    7.07
  
  
    20
    10-30cm
    6.99
    36.96
    13.997
  
  
    40
    30-60cm
    7.15
    36.03
    21.46
  
  
    80
    60-100cm
    7.55
    35.99
    30.19
  
  
    120
    100-150cm
    7.87
    36.17
    39.37
  
  
    180
    150-210cm
    8.36
    41.01
    50.14
  
  
    240
    210-270cm
    7.59
    39.36
    45.59
  
  
    300
    270-290cm
    6.34
    40.01
    12.68
  
  
    SWRLP
    0-290
     
     
    220.5



Table 5: The SWRLP in alfafa grass at the farmland.

Verification

The SWRULP theory can be approved in the field [9]. When the volumetric soil water content in the 0 to 290-cm soil layers is close to or equal to the wilting point, the soil water resource is equal to SWRUL and Caragana does not grow well because the caragana root expanded into 500 cm and the root water absorption depth is equal to root distribution depth plus soil moisture depth affected by roots, caragana can absorb some water from the soil layer below MID, but the absorbed water is smaller than canopy transpiration rate and cannot support plant grow well and forest or grass high quality sustainable development or high quality production of fruit or crops, and plant leaves may shift color from green to yellow and fall early before August in Caragana shrublands planted in the fish scale pit at the top of the Heici Mountain in 2003. Even the precipitation in the year was 623.3 mm, which was close to the maximum record of 634.7 mm in 1984 [12]. The theory could also be demonstrated based on field-measured growth data in 1 to 5 years Caragana shrub planted in the middle of Heici mountain. When the soil water resource level in the MID was equivalent to 222.8 mm since 15 May in 2006 (Figure 4b), the increment in Caragana height was only 4.3 cm among which, 96% of 4.3 (4.13 cm) was the amount of Caragana growth in the period from April 15 to May 15, and Caragana almost stop growing from May 15 (Figure 4c) because soil water resources in the MID of a five-year-old Caragana shrubland in 2006 was equivalent to 222.8 mm and the precipitation in 2006 was lower than the average annual precipitation (Figure 4a), indicating that the 222.8 mm in the MID was the SWRULP of Caragana in the semiarid loess hilly region. If the soil water supply from precipitation was inadequate (Figure 4a), soil water influenced Caragana growth considerably. Because the SWRULP was 222.8 mm in the Caragana shrubland of the semiarid region, the soil water resources decreased with Caragana growth. When the soil water resource is equivalent to SWRULP, soil water influenced Caragana growth greatly, and the plant water relationship should be regulated based on SWVCC in the key period of plant water relationship regulation to reduce the canopy interception rate and canopy transpiration rate. The first time of the regulation of the relationship is the start time, which is the 5th year after sowing [10]. Although soil water is concealed in the soil and is difficult to determine whether soil water storage at the MID is equivalent to SWRULP, height growth is a sensitive index that is easy to measure and can be used to assess whether soil water resources are equivalent to SWRULP. Therefore, a height growth of 5 cm can be considered as a value representing the SWRULP of Caragana in the region.

In the alfalfa grassland in 2015, when the soil water resources were equivalent to an SWRULP of 220.5 mm, the alfalfa wilted because alfalfa are soft-leaf plants. Saskatoon berries are good antidrought species and the plant water relationship in Saskatoon berries shrublands should not be regulated because they flower in the last 10 days of April, bear fruit in last 10 days of May, and mature in the first 10 days of July. In addition, it completes its growing season rapidly and halts growth before August, when the soil water resources are greater than SWRULP, showing that the relationship between soil water and plant growth should not be regulated on SWVCC in key period of plant water relationship regulation.

Discussion

The concept of soil water resources emerged in 1986 [4] after the concept of overall soil moistening [25]. Soil water resources can be defined as the water stored in the soil from the surface soil to the water table (Generalized soil water resources), the root zone (Narrow soil water resources), or the antecedent soil moisture plus the soil water supply from precipitation in the growing season for deciduous plants, or over a year for evergreen plants (Dynamic soil water resources). Soil water resources are renewable water resources and are components of water resources.

As the trees or plant grow and develop, soil water resource amounts reduce with an increase in annual plant growth, which may be observed in the form of height growth reductions. When the trees grow to a certain age, the leaf area index increases and the amounts of soil water uptake by plant roots keep rising and soil water supply decreases, which could cause a rapid decline in soil water content and soil water resources in the soil root zone, even if there are some increases following rainfall events. In addition, throughfall in forest land and soil water supply in root soil zone may dwindle since soil water mainly comes from precipitation through forest canopy and canopy interception increases because canopy density increases gradually in water-limited regions. Consequently, precipitation, soil evaporation, and plant transpiration influence soil water resource amounts, and non-native forest growth decreases soil water resources.

When the degree of soil drying reaches a certain limit where indicator plants cannot extract adequate water from the soil to meet the transpiration requirements of the plant, the soil drought has developed into severe soil desiccation [8,13,23], and the soil layer where the soil water content is equivalent to the wilting coefficient has become a DSL [9]. DSLs that have developed in soil layers below the MID become permanently dry soil layers, which ultimately result in the severe desiccation of soil, soil degradation, vegetation decline, and crop failure. Because permanent DSLs may cut off the link between soil water in the soil layers at higher levels than MID, and soil layers lower than MID, and influence the water cycle on land [36] and the sustainable use of soil water resources, severe desiccation of soil and soil degradation eventually lead to vegetation decline and crop failure. Therefore, it is critical to take steps to prevent the development of permanent DSLs as a soil water management strategy in water-limited regions.

The sustainability of forests planted in semiarid areas depends largely on the adaptability of the species and the management practices adopted based on the respective site conditions. Once a forest is established, cutting or thinning is a key management tool at the disposal of foresters; however, quantitative guidelines, based on key measurable processes, for the thinning of dryland forests remain scarce [37]. Consequently, there is a need to regulate the non-equilibrium relationship between soil water resources and plant growth by thinning some trees or cutting some branches, or leaves based on soil water vegetation carrying capacity (SWVCC) when the existing density surpasses the SWVCC to ensure that soil water resource are used sustainably.

To facilitate the control of soil degradation, a theory should be formulated and a suitable index developed for assessing the soil drought severity [9], particularly in environments where irrigation may not be practical due to factors such as inaccessible water tables.

Some of the soil water deficit indices include crop moisture index [30], soil moisture deficit index, evapotranspiration deficit index, and plant water deficit index [35]. Such drought indices can be divided into meteorological, hydrological, and agricultural drought indices [29]. Because most of the drought indices are based on meteorological variables [28] or on water balance equations, they hardly account for water deficit accumulation or soil water storage [27]. Therefore, such indices are not appropriate indices for evaluating soil drought severity in forests, grasslands, and farmlands in the water-limited regions such as the Loess Plateau of China, because soil drought is a natural phenomenon. Therefore, it is critical to develop novel indices that take into account factors such as the vertical distribution of roots in soil and how such factors influence the absorption of water in the soil profile.

There are two major criteria used to define soil water deficit: soil water resource use limit by plants (SWRULP) and lethal soil water resources. SWRULP is the limit of plants for the utilization of soil water resources. It is the soil water stored at MID when all the soil layers in the MID become DSLs, which implies that the soil water content in the MID is equivalent to the wilting coefficient and plant roots absorb water from soil layers deeper than MID. Lethal soil water resources represent the soil water stored in the root zone soil, at a level which the soil water content within the root zone soil is equivalent to the wilting coefficient. If the soil water resources are equivalent to lethal soil water resources and there is no timely supply of soil water from precipitation, plants would die because the plant-available soil water is used up in the root zone soil. The SWRULP in the Caragana shrubland was 222.3 mm when the wilting coefficient of 7.7% at the middle soil layer was used as the representative wilting coefficient of the entire soil profile to estimate SWRULP [12]. In fact, the SWRULP was 222.8 mm, because the wilting coefficients change with soil depth in the present study.

Briggs and Shantz (1912) emphasized the importance of the wilting coefficient. Richards and Weaver (1943) observed that soil water potential at wilting ranged from -1.0×105 to -2.0×105 MPa, with an average of approximately-15×106 MPa (15 bar). Therefore, the water content at -15×106 MPa is the point at which soil moisture usually becomes limited severely [22,31].

Because wilting coefficients are different for different plant species within a plant community because soil water potential at wilting ranges from -1.0 to - 20×106 Maps, wilting coefficients should be expressed based on the wilting coefficients of indicator plants in plant communities and changes in soil water potential at wilting under different vegetation types. If the soil water resources drop to the limit of soil water resources utilization by plant, the plant wilts and cannot recover the next day, indicating that the limit of soil water resources utilization by plant is too low, and it is necessary to fine-tune the soil water potential when wilting.

Because the wilting coefficient represents a minor range of soil water content [38], the low limit value of wilting coefficient could be used as the standard or plant soil water use index in every soil layer for estimating the SWRULP. In addition, because the centrifuge-based method can alter bulk density and over-estimate wilting coefficient, the pressure chamber method could be used to measure soil bulk density at different soil suctions and then estimate wilting coefficient, which would increase the precision of wilting coefficient.

Plants grow in complex environments, root distribution changes with soil depth, and plants absorb water from different soil depth and soil spaces. SWRULP is a superior soil water deficit index and it changes based on site condition and plant species, since it integrates soil texture, soil depth, infiltration depth, wilting point, and soil water management requirements, so that it better expresses severe soil drought in forest land.

SWVCC is the ability of soil water resources to support vegetation, expressed by the indicator plant or goal plant. When the soil water resources in the MID is equal to SWRULP, the plant water relation enter the critical period of water plant relation regulation [10,18]. The ending time of the critical period of water plant relation regulation is the ineffective time of water plant relation regulation, such as fruit stop expanding time. the SWVCC especially the SWVCC in critical period of plant water relation regulation decide the maximum yield and benefit [18].

Conclusion

Soil desiccation has an accumulative effect. When soil desiccation becomes severe and influences plant growth, it leads to soil degradation, vegetation decline, crop failure, and threatens the stability of nonnative forests and vegetation. To manage soil water resources effectively, it is necessary to understand and regulate the plant water relation on SWRULP and SWVCC in the critical period of plant water relation regulation.

The SWRULP was 222.8 mm in Caragana shrubland in the middle of Heici Mountain, 252.8 mm at the top of the semiarid region, and 220.5 mm in the alfalfa grassland in the Loess Plateau. When the soil water resources in the MID of 290 cm reached the limit, Caragana height growth was lower than 5 cm, which can be the alternative indicator value for SWRULP. The soil water resources would reach their limit 5 years after sowing, and the appropriate time to consider regulate the relationship between plant growth and soil water falls on the fifth year in the Caragana shrubland. While, alfalfa wilted, Saskatoon berries would grow well because key developmental stages such as flowering and fruit set fall under favorable conditions. The SWRULP theory could improve researchers’ understanding of plant water relation and determining the starting time of the key period of water plant relation regulation and selecting plants suitable for cultivation in a given site in water-limited regions. The SWRULP presents a foundation for the control of irreversible soil degradation and vegetation decline, sustainable use of soil water resource, agriculture high quality development in water-limited regions.

Author Statements

Acknowledgements

This project was supported by the National Science Foundation of China (Project No: 42077079,41271539,41071193) and Study on high quality sustainable development of soil and water conservation (A2180021002).

Competing Financial Interests Statement

There are no competing financial interests.

References

Download PDF

Citation:Guo Z. Plant Growth Development and Control in Water-Limited Regions. Ann Agric Crop Sci. 2024; 9(6): 1170.

Home

Journal Scope

editorial Board

Instruction for Authors

Submit Your Article